A Question of Scale

What started as a simple bug reported soon caused a pair of developers to question maths itself.

The Original Problem

It started innocently enough…

During testing, it was noticed that occasionally an order placed over Broker FIX received no acknowledgement. This was strange for a few reasons, not least because we hadn’t actually made any changes to the message flow around the system. Initial triaging revealed that this issue was localised. Only one test account was affected, and only for some of the orders it was placing.

The first thing we did was rule out anything external to the system—had the messages actually reached the front door? Yes. That was a good start. Knowing the messages had at least made it into the system meant it was likely to be a problem in one of the Java services.

Unfortunately, that is still a large surface area to have to investigate. So before jumping in, we wanted to know (roughly) which service we should focus our attention on. The handling of an order coming in via Broker FIX requires it to be passed between three components. It would normally look something like this:

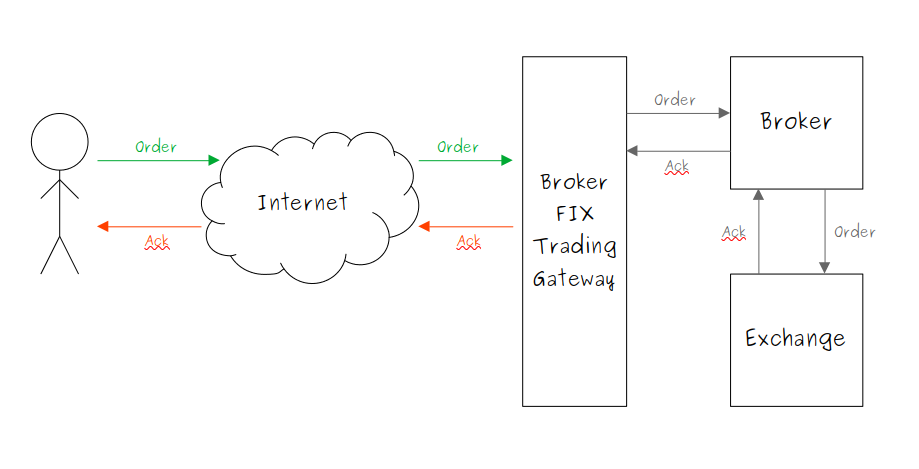
Our first action was to narrow down where the message was going AWOL. We knew that the place order instruction had been received by the gateway, and we knew that an acknowledgement had not been sent out. Everything between remained a mystery.

Fortunately, triaging an issue like this is easy. We design our systems to be deterministic. This means that as long as we have the original input we can reliably reproduce most behaviours. Rather than start with the incoming FIX message, tracing it through each component in turn, we decided to start in the middle and work out.

We started with the journals for events received by the Exchange. If the message appeared in these it would mean that the problem was sending the acknowledgment; if not, the problem was in processing the instruction. Searching for the order ID here turned up no results, so we took a step backwards and looked at the journals for events received by the Broker. This time we found an event that matched - which narrowed down the search space nicely.

Now we knew to look in the Broker, we could attach a debugger and replay the journals to see what is going on. We traced the message through until we reached a block of code that looked something like this:

class OrderManager
{
    /* ... snip ... */
    
    public void implicitClosePosition(final PlaceOrderInstruction instruction, final @UnitQty long openQuantity, /* ... snip... */)
    {
        final @UnitQty long availableToClose = calculateQuantityToCloseOnInstrumentPosition(instruction.getQuantity(), openQuantity);
    
        if (availableToClose != 0)
        {
            final OrderContext orderContext = this.orderContextFactory.fromPlace(instruction, /* ... snip ... */);
    
            orderContext.applyInflightClose(availableToClose);
            orderContext.onPlaceInstruction(instruction);
        }
    }
    
    /* ... snip ... */
}

The “implicit close position” feature was not something we were particularly familiar with, but the general principle was easy enough to grasp from the name. If an order is exactly equal-and-opposite to the account’s open position, we treat it as an attempt to close out that position.

The method body was also easy for us to comprehend. First, convert the quantity in contracts (@ContractQty) to a quantity in base units (@UnitQty) and then place the order if that quantity is non-zero. Nothing here stood out as being particularly interesting or relevant, so we decided to continue down the stack.

“Okay, let’s take a look inside onPlaceInstruction()”

We put a breakpoint at the start of onPlaceInstruction() and hit play…

Interlude: A Quick Note on Quantities

At this point it is worth noting the relationship between contract quantities and unit quantities.

For each order book we define a contract size that is used when sending or receiving quantities over FIX. Most order books have a contract size of either:

• 1 (i.e. an order of Buy 10 BTC/USD would be buying 10 BTC); or
• 10,000 (i.e. an order of Buy 10 EUR/USD would actually be buying 100,000 EUR).

The conversion is straightforward: unit_qty = contract_qty * contract_size.

We use The Checker Framework with the @ContractQty and @UnitQty annotations to maintain correctness when using these values.

Another parameter is quantity increment, which defines the granularity at which quantities can be specified. The quantity increment is specified as a @ContractQty, and can be used to allow or disallow fractional quantities. For example, one order book might allow increments of 0.1 whilst another may only allow increments of 1. If the contract quantity is set to 10,000, this would correspond to unit increments of 1,000 and 10,000 respectively.

Back To The Problem At Hand

… nothing happened!

To be more precise, the application continued running and never hit the breakpoint.

There is no return statement inside the if-statement, so we can rule out an early exit there. Could something have thrown? Theoretically this might be possible, but we probably would have seen this in the logs. This really only left one option—we never entered the body if-statement.

The lack of an else-clause attached to the if in the earlier snippet had raised some red-flags, but we hadn’t expected it to be a problem:

• the order in question was for a buy order with @ContractQty of 10.
• the order book specified a contract size of 1, which should lead to a @UnitQty also of 10.
• because 10 != 0 we expect to enter the body of the if and thus we should hit the breakpoint!

We started debugging again, this time placing a breakpoint outside the if-statement.

It turned out that availableToClose was in fact 0, despite the quantity being 10.

“Curious…”

Apparently calculateQuantityToCloseOnInstrumentPosition() disagreed on the conversion from contracts to units, although it was not immediately clear why. Thankfully, we were still debugging and so we dropped the frame and stepped into the calculateQuantityToCloseOnInstrumentPosition() method:

static @UnitQty long calculateQuantityToCloseOnInstrumentPosition(final @ContractQty long quantity)
{
    final @UnitQty long requestedQuantity = this.orderBook.contractSpecification.contractsToUnitQuantity(quantity);
    final @UnitQty long roundedQuantity = this.orderBook.toClosestValidOrderQuantity(requestedQuantity);
    return roundedQuantity;
}

It turned out calculateQuantityToCloseOnInstrumentPosition() was pulling double-duty:

• it converts contracts to units, (as advertised by the method signature); but also
• it ensures the calculated unit quantity is valid according to the order book’s quantity increment.

This second duty was something we hadn’t anticipated at first; however, it was not immediately obvious why this would matter. We assumed that the quantity would be validated higher up the stack¹ but maybe not. Was this just a case of missing validation, and an invalid quantity that had slipped through?

We went to the database to check.

The quantity increment for the order book in question was 10. In our experience quantity increments are normally fractions of 1 (1, 0.1, 0.01 etc) but we accepted it might not always be so. This was curious but was not a smoking gun. Regardless, it was not enough to explain the 0 we were seeing: 10 rounded to the nearest increment of 10 is 10… isn’t it?

Turns out, it isn’t².

We stepped through and found requestedQuantity resolved to 10 as expected, and it was roundedQuantity that came out as 0.

Another dropped frame, and another step-into brought us inside toClosestValidOrderQuantity():

@UnitQty long toClosestValidOrderQuantity(final @UnitQty long unitQuantity)
{
    final BigDecimal quantity = contractSpecification.unitToContractQuantityAsBigDecimal(unitQuantity);
    final BigDecimal roundedQuantity = MathUtil.roundToMultipleOf(quantity, getOrderQuantityIncrement(), RoundingMode.ROUND_HALF_EVEN);
    return contractSpecification.contractsToStandardisedUnitQuantity(roundedQuantity);
}

Nothing here looks overtly suspicious. Stepping over the lines we saw the same pattern as previously: quantity was 10 (just now in BigDecimal form) and, again, roundedQuantity was 0. This led us inside roundToMultipleOf(), to another fairly plain looking method body:

public static BigDecimal roundToMultipleOf(final BigDecimal value, final BigDecimal increment, final int roundingMode)
{
    BigDecimal multiples = value.divide(increment, RoundingMode.FLOOR);
    multiples = multiples.setScale(0, roundingMode);
    return multiples.multiply(increment).setScale(increment.scale());
}

This is about as deep as we can go in our code—we are now dealing exclusively with standard Java objects. We started getting worried that we’d just missed something obvious higher up, but as Magnusson would have said: “I’ve started, so I’ll finish”.

The debugger is already helpfully confirming the things we previously thought to be true are still true: value is 10 and increment is 10. Unless something strange is happening with the .setScale() calls—a possibility we have yet to rule out—we are now just performing basic maths.

(Not to brag, but I got an A in A-level maths, was feeling pretty confident at being able to divide and multiply by 10!)

Then things got weird…

I Forgot How To Maths

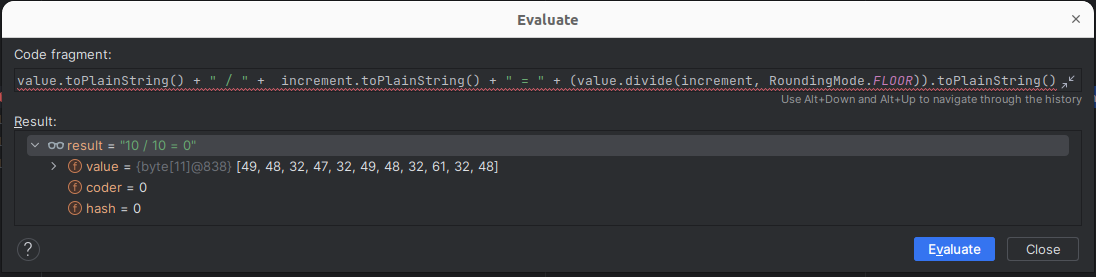
This was not what we were expecting to happen! (Maybe I didn’t deserve that A after all?)

“… did I just forget how to do maths?!”

Our first thought was that, given these numbers were coming in as BigDecimals, maybe there was some issue with precision. We played about with various rounding modes in the evaluator. One of the more interesting results came from using RoundingMode.UNNECSSARY. The JVM disagreed—it was very insistent that, when dividing our 10 by our other 10, rounding was necessary.

Eagle-eyed readers might notice that in the debugger we’re calling .toPlainString() on the BigDecimal. This was because the regular .toString() returned the number as 1E+1 and this made it slightly harder to read. At first, we had not thought this important; however, as we began to run out of threads to pull we turned our attention in this direction. Maybe this representation was somehow concealing a loss of precision?

What followed was a protracted (and ultimately relatively uninteresting) investigation into whether 1e1 and 10 are the same. It turned out that they are equivalent but are not equal. To be more specific: .compareTo() returns 0 whilst .equals() returns false. This is because the “scale” of the numbers is different (-1 and 0 respectively). Normalising the scale made the comparison succeed.

A Question Of Scale

Despite being mostly a wild goose chase, this investigation brought our attention to the scale of the BigDecimals. Out of curiosity, we ran some simple tests performing division on BigDecimal.TEN setting different scales:

class Scratch
{
    private static void test(final BigDecimal left, final BigDecimal right, final RoundingMode round)
    {
        System.out.println(left.toPlainString() + " / " + right.toPlainString() + " = " + left.divide(right, round).toPlainString());
    }
    
    public static void main(String[] args)
    {
        final BigDecimal ten = BigDecimal.TEN;
        test(ten, ten, RoundingMode.FLOOR); // => 10 / 10 = 1
        test(ten.setScale(1), ten.setScale(1), RoundingMode.FLOOR); // => 10.0 / 10.0 = 1.0
        test(ten.setScale(1), ten.setScale(10), RoundingMode.FLOOR); // => 10.0 / 10.0000000000 = 1.0
        test(ten.setScale(10), ten.setScale(1), RoundingMode.FLOOR); // => 10.0000000000 / 10.0 = 1.0000000000
        test(ten.setScale(10), ten.setScale(10), RoundingMode.FLOOR); // => 10.0000000000 / 10.0000000000 = 1.0000000000
        test(ten.setScale(-1), ten.setScale(-1), RoundingMode.FLOOR); // => 10 / 10 = 0
    }
}

Ah-ha!

We learned that the result of operations on a BigDecimal inherit the scale from the BigDecimal on the left-hand side³.
… but what does a negative scale even mean?
… and why does that result in 0?
… also, where did that -1 even come from?

The JavaDoc for .setScale() is not particularly forthcoming regarding negative scales:

Returns a BigDecimal whose scale is the specified value, and whose unscaled value is determined by multiplying or dividing this BigDecimal’s unscaled value by the appropriate power of ten to maintain its overall value. If the scale is reduced by the operation, the unscaled value must be divided (rather than multiplied), and the value may be changed; in this case, the specified rounding mode is applied to the division.

Returns: a BigDecimal whose scale is the specified value, and whose unscaled value is determined by multiplying or dividing this BigDecimal’s unscaled value by the appropriate power of ten to maintain its overall value.

Luckily this has come up on StackOverflow at least once:

Yes, it makes sense to set the scale to a negative number in certain situations. That just means that the number is rounded to the nearest 10 to the -scale number, or just 10 in this case.

This explains why the division returns 0: 10 / 10 is 1, but it is rounded to the nearest 10, which in this case is 0. (This is true for almost all rounding modes; however, if we use a rounding mode of RoundingMode.CEILING the division rounds up to 10.)

This left us with one final question: where did the scale of -1 come from?

We returned to the Java code, in particular to this line:

final BigDecimal roundedQuantity = MathUtil.roundToMultipleOf(quantity, getOrderQuantityIncrement(), RoundingMode.ROUND_HALF_EVEN);

The getOrderQuantityIncrement() method seemed like it could be interesting, but turned out to be just a regular getter. The actual value was being set elsewhere; we ultimately traced it back to this method:

public BigDecimal unitToContractQuantityAsBigDecimal(final @UnitQty long quantity)
{
    final BigDecimal standardisedUnits = BigDecimal.valueOf(quantity).setScale(MAX_ALLOWED_QUANTITY_SCALE, RoundingMode.UNNECESSARY);
    return standardisedUnits.divide(standardisedUnitsToContractsDivisor, RoundingMode.UNNECESSARY).stripTrailingZeros();
}

We saw an explcit call to .setScale(), but the constant, MAX_ALLOWED_QUANTITY_SCALE is set to 8. Since we had already established that .divide() inherits the scale, this left us looking at .stripTrailingZeros().

In Java’s defence, this time the JavaDoc is very explicit about the expected behaviour:

Returns a BigDecimal which is numerically equal to this one but with any trailing zeros removed from the representation. For example, stripping the trailing zeros from the BigDecimal value 600.0, which has [BigInteger, scale] components equals to [6000, 1], yields 6E2 with [BigInteger, scale] components equals to [6, -2]. If this BigDecimal is numerically equal to zero, then BigDecimal.ZERO is returned.

Returns: a numerically equal BigDecimal with any trailing zeros removed.

As we had already established that our quantity increment in this case was 10, the returned value of [1, -1] (or 1E+1) makes sense. But it probably wasn’t the intention of the original author of this code.

At this point, we were fairly happy that we understood both the trigger and the root cause of the issue. We also had some ideas on how to resolve it.

“How come we’ve never seen this before?”

This issue manifested due to two conditions being true:

• an “implicit close position” order was placed with a size exactly equal to the order book’s quantity increment; and
• the order book’s quantity increment was a power of 10 greater than 1.

This code was originally written in 2016. We hoped that if this had ever manifested in production, we would have heard about it. But hope is not a strategy. We needed to be sure. Thankfully in production no order books had an increment of 10 (or, in fact, anything larger than 1). Fundamentally, this whole issue was down to a misconfiguration!

Mitigation and Remediation

The mitigation was to update the order book configuration. Originally the order book had a contract size of 1 and a quantity increment of 10; we changed it to a contract size of 10 with a quantity increment of 1. This preserved the semantics of only being able to place orders in tens-of units.

After resolving the immediate problem, we wanted to make sure this configuration would not cause problems in the future.

Our first step was to reproduce this scenario via a test. This was mostly trivial, as we had already collected all the information we needed. Even so, we were still hit one more stumbling block along the way—it turned out that the side of the order was important. We were unable to reproduce the behaviour with a sell order (modeled with a quantity of -10).

Once the test was in place (and failing) we started to think about the best way to fix the root cause. Our initial thought was to just remove the call to .stripTrailingZeros(); however, git log showed us that it had been put in deliberately. Unfortunately, the exact reasoning behind why it had been put in was vague and unclear. We didn’t want to remove this without understanding why it was added, instead we settled for something more verbose:

public BigDecimal unitToContractQuantityAsBigDecimal(final @UnitQty long quantity)
{
    final BigDecimal standardisedUnits = BigDecimal.valueOf(quantity).setScale(MAX_ALLOWED_QUANTITY_SCALE, RoundingMode.UNNECESSARY);
    final BigDecimal strippedStandardisedUnits = standardisedUnits.divide(standardisedUnitsToContractsDivisor, RoundingMode.UNNECESSARY).stripTrailingZeros();
    return strippedStandardisedUnits.setScale(Math.max(strippedStandardisedUnits.scale(), 0));
}

This preserved the intention of the original code and also made it safe for any quantity increment greater than 1. We re-ran our test—it passed.

Final Thoughts

This trigger for this bug was a combination of two specific conditions: a specific “implicit close position” order on strangely configured order book. Could we have caught this in an automated test? Technically: yes; realistically: probably not. Complex systems will always have gaps like this. However, this doesn’t mean that there are things we could have done better, and can do better in the future.

The if-statement with no else-clause was eyebrow-raising even before it was identified as being relevant to our issue. In a truly test-driven development process, at least one test case would exist to justify it. Sadly, that was not true here, and that potentially makes it a candidate for deletion.

This bug also raised a wider question of validation around the parameters that can be set on an order book. Should a quantity increment of 10 ever have been accepted by the system? If not, we should add validation rejecting this in future; if so, we need to ensure we have tests using a value of 10 (but even then, we know we will never catch everything).

At least by identifying these gaps in test coverage we can make a start at plugging them.

… and maybe I don’t need to hand my A-level result back after all?